Recently, Ξ over at the 360 blog wrote about hyperbolic light (which was inspired by the article, “The Shape of Lamp Shade Shadows” by Kenneth E. Horst, The Physics Teacher, Volume 39, March 2001). They were looking at the pattern of light on the wall emitted by a desk lamp with a cylindrical lampshade. They observed that the shape of the light was a hyperbola. The reason for this, as Ξ points out, is that the bulb and lampshade form a cone of light and the wall is a plane slicing that cone. As we see in the third picture below, such a plane cuts the cone in a hyperbola.

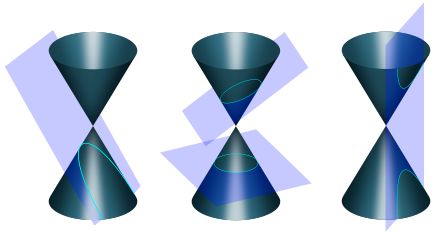It stands to reason that we can get the other conic sections—the parabola (left), circle (center, bottom) and ellipse (center, top)—by tilting the lamp.

As it turned out I was teaching about conic sections last week (they arise as traces of quadric surfaces), so I decided I had to show this to my class. I walk to work and didn’t want to carry a lamp in to school, so I decided to make a portable version.

My first thought was to use a flashlight. But flashlights are designed to focus light to a single point as much as possible. They don’t make a nice cone. Then I decided to make a “lampshade” (shown below) for my flashlight out of a stiff piece of paper (I used a file folder). Ideally there would be a single point source of light at the bottom of the shade, but this won’t be the case because of the parabolic reflector in the flashlight. After a little experimentation I found that the longer the “shade,” the better the cone of light. Also, to make a circular cone, the shade needs a good circular opening at the other end (not squashed or kinked)—it took a little fussing to get things the way I wanted them.

In class class I drew the blinds, turned off the lights, and shined my light on the projector screen. It worked pretty well. I could make a good circle (point the flashlight directly at the wall), an ellipse (tip the light up a little), a parabola (tip it farther), and half a hyperbola (farther still)!

The students thought it was pretty cool (I have a good bunch this semester!).

[Conic section image by Pbroks13, published under the Creative Commons Attribution 3.0 Unported License.]