Volumes of n-dimensional balls

We all know that the area of a circle is ${\pi r^{2}}$ and the volume of a sphere is $\frac{4}{3}\pi r^{3}$ , but what about the volumes (or hypervolumes) of balls of higher dimension?

For a fun exercise I had my multivariable calculus class compute the volumes of various balls using multiple integrals. The surprising results inspired this post.

First some terminology. An ${(n-1)}$ -dimensional hypersphere (or ${(n-1)}$ -sphere) of radius ${R}$ is the set of points in ${\mathbb{R}^{n}}$ satisfying ${x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=R^{2}}$ (I’ll place the center at the origin for simplicity). For example, a 0-sphere is the two-point set ${\{\pm R\}}$ on the real number line, a 1-sphere is a circle of radius ${R}$ in the plane, and a 2-sphere is a spherical shell of radius ${R}$ in 3-dimensional space.

An ${n}$ -dimensional ball (or ${n}$ -ball) is the region enclosed by an ${(n-1)}$ -sphere: the set of points in ${\mathbb{R}^{n}}$ satisfying ${x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}\le R^{2}}$ . For example, a 1-ball is the interval ${[-R,R]}$ , a 2-ball is a disk in the plane, and a 3-ball is a solid ball in 3-dimensional space.

It is possible to define “volume” in ${\mathbb{R}^{n}}$ —in ${\mathbb{R}}$ it is length, in ${\mathbb{R}^{2}}$ it is area, in ${\mathbb{R}^{3}}$ it is ordinary volume, and in ${\mathbb{R}^{n}}$ it is hypervolume. Let ${V_{n}(R)}$ denote the volume of the ${n}$ -ball of radius ${R}$ .

$\displaystyle \begin{array}{|c|c|c|c|} \hline n & \text{equation} & \text{shape} & V_{n}(R) \\ \hline 1 & x^2\le R^2 & \text{interval}& 2R\text{ (length)} \\ \hline 2 & x^2+y^{2}\le R^2 & \text{disk} & \pi R^{2}\text{ (area)} \\ \hline 3 & x^2+y^{2}+z^{2}\le R^2 & \text{ball} & \frac{4}{3}\pi R^{3}\text{ (volume)} \\ \hline 4 & x_{1}^2+x_{2}^2+x_{3}^2+x_{4}^2\le R^2 & \text{4-dimensional ball} & \text{?? (hypervolume)} \\ \hline \vdots &\vdots & \vdots & \vdots \\ \hline \end{array}$

It turns out that the volumes of ${n}$ -balls satisfy the following remarkable recursion relation. (I’ll prove this relation at the end of the post.)

$\displaystyle V_{1}(R)=2R,\, V_{2}(R)=\pi R^{2},\,\text{and }V_{n}(R)=\frac{2\pi R^{2}}{n}V_{n-2}(R),\text{ for }n\ge 3.$

It is not difficult to use this recurrence relation to obtain a formula for ${V_{n}(R)}$ . In particular, when ${n}$ is even $V_{n}(R)=\frac{2^{\frac{n}{2}}\pi^{\frac{n}{2}}R^{n}}{2\cdot 4\cdot 6\cdots n}=\frac{\pi^{\frac{n}{2}}R^{n}}{(\frac{n}{2})!}$ and when ${n}$ is odd $V_{n}(R)=\frac{2^{\frac{n+1}{2}}\pi^{\frac{n-1}{2}}R^{n}}{1\cdot 3\cdot 5\cdots n}$ . (If you know what the gamma function is you can express this as a single function, $V_{n}(R)=\frac{\pi^{\frac{n}{2}}R^{n}}{\Gamma(\frac{n}{2}+1)}.$ )

The volumes of the ${n}$ -balls in the first 15 dimensions are given in the following table.

$\displaystyle \begin{array}{|c|c|l|} \hline n & V_{n}(R) & V_{n}(1) \\ \hline 1 & 2R& 2 \\ \hline 2 & \pi R^{2}& 3.141592654\ldots \\ \hline 3 & \displaystyle\frac{4\pi R^{3}}{3}& 4.188790205\ldots\\ \hline 4 & \displaystyle\frac{\pi^{2}R^{4}}{2}&4.934802201\ldots\\ \hline 5 & \displaystyle\frac{8\pi^{2}R^{5}}{15}&5.263789014\ldots\\ \hline 6 & \displaystyle\frac{\pi^{3}R^{6}}{6}&5.16771278\ldots\\ \hline 7 & \displaystyle\frac{16\pi^{3}R^{7}}{105}& 4.72476597\ldots\\ \hline 8 & \displaystyle\frac{\pi^{4}R^{8}}{24}& 4.058712126\ldots\\ \hline 9 & \displaystyle\frac{32\pi^{4}R^{9}}{945}& 3.298508903\ldots\\ \hline 10 & \displaystyle\frac{\pi^{5}R^{10}}{120}& 2.55016404\ldots\\ \hline 11 & \displaystyle\frac{64\pi^{5}R^{11}}{10395}& 1.884103879\ldots\\ \hline 12 & \displaystyle\frac{\pi^{6}R^{12}}{720}& 1.335262769\ldots\\ \hline 13 & \displaystyle\frac{128\pi^{6}R^{13}}{135135}& 0.910628755\ldots\\ \hline 14 & \displaystyle\frac{\pi^{7}R^{14}}{5040}& 0.599264529\ldots\\ \hline 15 & \displaystyle\frac{256\pi^{7}R^{15}}{2027025}& 0.381443281\ldots\\ \hline \end{array}$

If you look at the volumes of the unit balls you’ll see they increase at first, reaching a maximum in dimension 5. Then they decrease and tend to zero as the dimension goes to infinity. Strange!

First, what is special about dimension 5? Why is the maximum achieved in this dimension? It turns out that there is nothing special about dimension 5. Below is a GeoGebra applet that allows you to adjust the radii of the balls. As we can see, the maximum volume is not always attained by the ball in dimension 5. Indeed, as the radius increases, the maximum volume occurs in higher dimensions. As John Moeller points out, the powers of ${R}$ in the numerator try to make ${V_{n}(R)}$ an increasing function, however the factorials in the denominator always dominate in the end.

Second, what is the intuition behind this limit of zero? One way to see this is to observe that to be on the boundary of the unit ${n}$ -ball, we must have ${x_{1}^{2}+x_{2}^{2}+\cdots+x_{n}^{2}=1}$ , but for this to happen when ${n}$ is large, most of the ${x_{i}}$ ‘s must be very close to zero. For example, the line ${x_{1}=x_{2}=\cdots=x_{n}}$ intersects the ${n}$ -sphere at ${\pm(\frac{1}{\sqrt{n}},\ldots,\frac{1}{\sqrt{n}})}$ . On the other hand, the corresponding corners of the hypercube that inscribes the sphere are at ${\pm(1,\ldots,1)}$ , ${\sqrt{n}}$ units from the origin. Thus the sphere fills up less and less of the hypercube that contains it. (Notice that the circumscribed hypercube has volume ${2^{n}}$ , while inscribed hypercube has volume ${2^{n}/n^{\frac{n}{2}}}$ .)

My colleague informed me that this zero limit is related to the curse of dimensionality in statistics. Volume increases rapidly as dimension increases, so it requires many more data points to get a good estimate. As Wikipedia points out, “100 evenly-spaced sample points suffice to sample a unit interval with no more than 0.01 distance between points; an equivalent sampling of a 10-dimensional unit hypercube with a lattice with a spacing of 0.01 between adjacent points would require ${10^{20}}$ sample points.”

Proof

Now I will prove the recurrence relation that I gave above.

Clearly the relation is true for ${n=1}$ and ${n=2}$ . Suppose ${n\ge 3}$ .

First recall that if a solid in ${n}$ -dimensional space is scaled by a factor of ${k}$ , then its volume increases by a factor of ${k^{n}}$ . In particular, this implies that

$\displaystyle V_{n}(R)=V_{n}(1)R^{n}.$

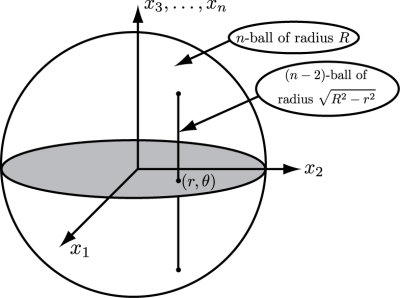
Observe that the intersection of the ${(x_{1},x_{2})}$ -plane with the ${n}$ -ball is a disk of radius ${R}$ centered at the origin (see image below). Use polar coordinates to describe points in this disk. Then the perpendicular cross section of the ${n}$ -ball at the point ${(r,\theta)}$ is an ${(n-2)}$ -ball of radius ${\sqrt{R^{2}-r^{2}}}$ .

Thus we can compute ${V_{n}(R)}$ by integrating ${V_{n-2}(\sqrt{R^{2}-r^{2}})}$ over the disk. We do so using polar coordinates.

$\displaystyle \begin{array}{rcl} V_{n}(R)&=&\displaystyle \int_{0}^{R}\int_{0}^{2 \pi}V_{n-2}\big(\sqrt{R^{2}-r^{2}}\big)r\,d\theta\,dr \\ &=&\displaystyle \int_{0}^{R}\int_{0}^{2 \pi}V_{n-2}(1)(\sqrt{R^{2}-r^{2}}\big)^{n-2}r\,d\theta\,dr\\ &=&\displaystyle V_{n-2}(1)\int_{0}^{R}r\big(R^{2}-r^{2})^{\frac{n-2}{2}}\theta\Big|_{0}^{2\pi}\,dr\\ &=&\displaystyle 2\pi V_{n-2}(1)\int_{0}^{R}r(R^{2}-r^{2})^{\frac{n-2}{2}}\,dr\\ &=&\displaystyle -\frac{2\pi}{n} V_{n-2}(1)(R^{2}-r^{2})^{\frac{n}{2}}\Big|_{0}^{R}\\ &=&\displaystyle 2\pi V_{n-2}(1)\frac{R^{n}}{n}\\ &=&\displaystyle \frac{2\pi R^{2}}{n}V_{n-2}(R) \end{array}$

27 Comments

Mark Reid says:

May 9, 2010 at 2:01 pm

Great post!

This is another good example of why you have to be careful when dealing with high-dimensional geometry. I posted a similar counter-intuitive result to do with the relative volumes of cubes and spheres a while back.

Dave Richeson says:

May 10, 2010 at 3:10 pm

Wow, that is really excellent. Thanks for sharing the link.

Farbod Shokrieh says:

May 9, 2010 at 4:43 pm

This volume computation is done in the book Symmetric Bilinear Forms (By Milnor, Husemoller) as part of the full classification of indefinite integral inner product spaces (by their rank, type, and signature).

There, it is shown that there is indeed something spacial about n=5; using Minkowski’s convex body theorem, it is more natural to look at the behavior of $4/(V_n(1))^{2/n}$, which is larger than 2 for n>4, which makes the solution to the classification problem essentially different for n=5.

Farbod Shokrieh says:

May 9, 2010 at 8:12 pm

n=5 is “n > = 5” at the end of my previous comment.
Dave Richeson says:

May 10, 2010 at 8:30 am

Thanks. Very interesting. I’ll be sure to track down that reference.

Paul says:

May 9, 2010 at 4:49 pm

Interesting post. I have to say though that comparing length to area to volume to hypervolume and so on makes little sense, IMHO it would be better to plot the fraction of the hypercube each sphere occupies.

(there is a typo in second table should be R^3 in n=3)

Dave Richeson says:

May 10, 2010 at 8:32 am

I agree—we’re comparing apples to oranges to bananas here (which doesn’t make it less fun to do). I like your idea. I’ll have to give that a try when I get a chance.

Thanks for catching the typo. It is fixed now.

Qiaochu Yuan says:

May 9, 2010 at 8:29 pm

There was a nice MathOverflow question about the volume tending to zero which attracted a lot of great answers.

Dave Richeson says:

May 10, 2010 at 8:34 am

Wow. Excellent. Thanks for providing that link.

sherifffruitfly says:

May 12, 2010 at 11:55 pm

Fleming’s 5.9, Functions of Several Variables has a very nice discussion of this. Not the curse of dimensionality bit, though – that was a nice tie-together.

sherifffruitfly says:

May 13, 2010 at 9:58 am

Wait a minute.

“Volume increases rapidly as dimension increases”

Now look at your dim/vol plot.

Huh?

Dave Richeson says:

May 13, 2010 at 12:45 pm

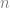Yes, that’s not so clear. Here’s what I meant: a hypercube of side length $x$ in dimension $n$ has hypervolume $x^n$ . So if $x>1$ and $n$ is large, then this volume is very large.
1. sherifffruitfly says:
  
  May 13, 2010 at 1:58 pm
  
  Ah – different object – gotcha.
  
  That suggests a possibly interesting investigation I haven’t seen before: how does the volume of the unit n-cube or sphere vary with the *metric*. (You changing objects from sphere to cube suggested metric change to me because under other metrics, “circles” become “squares”.)
  
  I would be curious to see a discussion of what, if anything, general could be said about the measure of typical sets as one varies the metric – especially with convergent sequences of metrics and the like. Knew I should’ve taken that functional analysis class. :P

DavidC says:

May 13, 2010 at 11:20 pm

Really interesting. Thanks.

Pingback: More Press « Random Walks

Matt McDonnell says:

June 7, 2010 at 4:23 pm

Another Math Overflow posting that had some interesting thoughts on thinking in higher dimensions. Particularly interesting post by Terry Tao:
“For instance, the fact that most of the mass of a unit ball in high dimensions lurks near the boundary of the ball can be interpreted as a manifestation of the law of large numbers, using the interpretation of a high-dimensional vector space as the state space for a large number of trials of a random variable.”

Dave Richeson says:

June 7, 2010 at 4:46 pm

Thanks! I’ve just started reading MathOverflow—I’ve known about it for a while, but have been too busy to dive in. It is great. Thanks for pointing this question out to me.

Pingback: Volumes of generalized unit balls — The Endeavour

AGNOSTIKOS says:

July 12, 2010 at 6:39 pm

Re string theory– if the visible universe is a 9-d object w/ 3d of ~ (10^26)m and 6d of ~(10^-35)m, its diameter is then ~(10^-14.67)m, about the diameter of a proton. No part of our universe is any farther than this from any other part- considered hyperspatially. This may be a boring and inconsequential factoid to STists, but it’s bogglesome enough that the pop-sci press should be all over it.

Pingback: Some peculiarities of higher dimensional spaces « Republic of Mathematics

Hawaii says:

December 3, 2012 at 1:58 am

For n=5, pi should be squared, not cubed.

Dave Richeson says:

December 4, 2012 at 6:32 pm

Thanks! Fixed.

Pingback: Mattebloggen » Blog Archive Bollvolymer i n dimensioner » Mattebloggen

Pingback: Surface Areas and Volumes of Hyperspheres | Rob Hubbard's Blog

Kishore Swaminathan says:

October 18, 2013 at 4:16 pm

What happens when x -> ∞? In other words, what is the volume of a sphere of infinite radius and infinite dimensions? Is it still zero?

Kevin Iga says:

March 3, 2014 at 1:19 am

There’s a nice proof without induction that uses the gamma function directly, in Peskin & Schroder’s Quantum Theory of Fields. Remember the proof of the integral of a gaussian, using 2d in polar coords? This does the same in reverse. Take e^{-x_1^2 – … – x_n^2} and integrate over R^n. In cartesian coords you get pi^(n/2). Switch to polar coords and you get the formula for the surface area of a sphere times a Gamma function. Integrate surface area to get (hyper-) volume.

Vincent says:

April 18, 2014 at 3:28 am

Nicely written and easy to understand, tnx! It is interesting to see that you mentioned the connection to ‘the curse of dimensionality’ in statistics and machine learning. Indeed this phenomena makes it difficult to train classifiers and regressions in highly dimensional spaces because most of the data lives in ‘the corners’ of the feature space (hypercube) instead of being at the center (within the hypersphere). I recentely wroten an intuitive explanation about this, and the link between your post and the curse of dimensionality: http://www.visiondummy.com/2014/04/curse-dimensionality-affect-classification/

Comments are closed.

Share this:

Related

27 Comments