Yesterday I came a across a new (new to me, that is) proof of the irrationality of . I found it in the paper “Irrationality From The Book,” by Steven J. Miller, David Montague, which was recently posted to arXiv.org.
Apparently the proof was discovered by Stanley Tennenbaum in the 1950’s but was made widely known by John Conway around 1990. The proof appeared in Conway’s chapter “The Power of Mathematics” of the book Power, which was edited by Alan F. Blackwell, David MacKay (2005).
It is a proof by contradiction. Suppose for some positive integers
and
. Then
. Geometrically this means that there is an integer-by-integer square (the pink
square below) whose area is twice the area of another integer-by-integer square (the blue
squares).
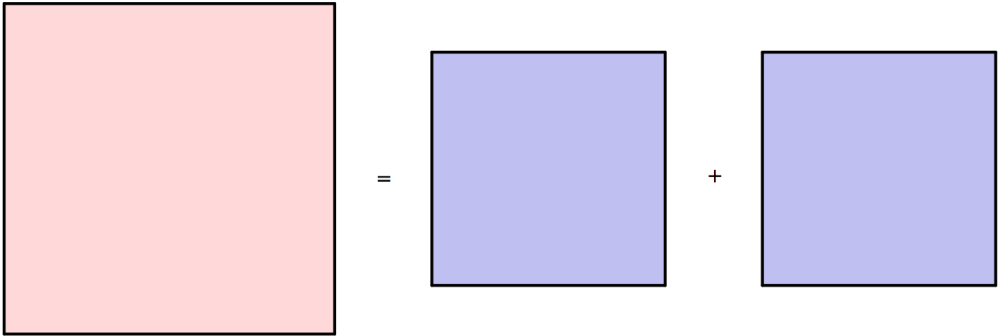
Assume that our square is the smallest such integer-by-integer square.
Now put the two blue squares inside the pink square as shown below. They overlap in a dark blue square.

By assumption, the sum of the areas of the two blue squares is the area of the large pink square. That means that in the picture above, the dark blue square in the center must have the same area as the two uncovered pink squares. But the dark blue square and the small pink squares have integer sides. This contradicts our assumption that our original pink square was the smallest such square. It must be the case that is irrational.
[Note: the squares in the pictures almost work. They are and
. As Conway points out,
. Indeed
.]
If you want to see more examples, look at Miller and Montague’s paper “Irrationality From The Book.” They extend this idea to give geometric proofs that ,
,
, and
are irrational.
Also, Cut-the-Knot has 19 proofs of the irrationality of (including this one).
I just read (literally a few short hours ago) an almost identical proof (except done with a right triangle) in The Calculus of Friendship by Steven Strogatz. Thanks for posting this version!
I am Stanley Tennenbaum’s youngest son and partially responsible for getting the word out about this proof after he died in May 2006, in Princeton.
Sadly, John Conway got a number of facts wrong in the book version of this proof and, previously, in some of his online versions of it.
There is absolutely no question that my father discovered this in the early 50s. Note the website:
http://www.cancerdisaster.org
Soon, thousands of pages of his unpublished math and educational views will appear online, some polished, most of it notes, albeit a lot taken from diary entries and other handwritten sources.
There will also be audio and video.
Note the two quotes by Kurt Goedel that appear on the very bottom right hand side of the above site, taken from two letters of recommendation. Only one page of this site is up now, but that should change in a few weeks.
The true story of my father is wild beyond imagination. He was an extremely controversial figure, but probably the closest person to Goedel, both personally and professionally, certainly from the late 60s until Goedel died. This is well known among the top logicians and mathematicians many of whom met Goedel through my dad (indeed, Conway himself, by his own words, on videotape at a conference in my father’s honor/memory, met Goedel in a meeting arranged by my dad).
I am now 53 and witnessed him showing this beautiful proof to hundreds of people during my lifetime, including Hans Bethe, the famous physicist, when we met up with him in Cornell, in 1978.
Many people knew about it, and many did not. Again, sadly, it appears that Conway, since he had not heard about it, thought that my dad JUST found it, because my father told Conway the proof in the early 90s. But many others saw it many many decades earlier. My brother remembers it from the 50s and so does Prof. Nerode, from Cornell who recently told me in no uncertain terms that it came from the early 50s when my dad was at the University of Chicago.
More interesting, however, than any of the above talk about dates and famous people, are Goedel’s amazing conversation notes that he took during conversations with my dad. When they are finally fully translated they will be fascinating beyond measure because the range of topics discussed was extraordinarily broad.
In any case, I’ll have plenty to say about this, and other matters, on the website.
Thanks for posting it — not simply for the attribution to my father (although he certainly deserves it) — but for getting the word out about a proof that is simply beautiful. It can inspire others, especially young people, to learn about mathematics.
My dad thought that MOST of math will be reduced, at some point, to proofs of this nature, where the essential ideas are crystal clear and the proofs are radically simplified.
I can still remember him repeating to me:
“Always a picture, always a picture…..”
Peter Tennenbaum October 26, 2009
Rochester, NY
Peter,
Thank you for sharing all of this. Please let me know by email when your website is live. It sounds like it will be a wonderful resource.
Dave
Prof. Richeson,
I would like to point out that the paper “Irrationality From The Book,” by Steven J. Miller, David Montague, which was recently posted to arXiv.org has just been updated (see version 2); it is now far more accurate, historically.
Conway did indeed publicize this proof, but he did this 40 years after it was discovered and AFTER my father had ALREADY publicized it himself, albeit orally, by telling hundreds of people, mostly students, but many, many mathematicians. It is a shame that he did not publish it himself before he died. But he died suddenly, without any warning and he had spoken often about publishing it, especially as he got older.
It is also a shame that more people did not tell others about it after hearing it from my dad. Forty years is a long time and, if they had, then the whole mathematical community would surely have seen this proof long ago and it probably would have already appeared in many books and many papers.
Another point:
Your reference to Conway, above, with respect to the size of the squares, in my father’s proof, makes little sense, at least to me. Moreover, from my point of view, Conway’s OWN use of these numbers “17 and 12” makes little sense in his chapter titled “The Power of Mathematics” in the book “Power”.
Why?
Well, first of all, it is indeed true that 17/12 is a close approximation to the square root of two. But so what?
Since the rationals are everywhere dense on the real line, it is hardly surprising that some of them make good approximations to the square root of two or, for that matter, any real number whether irrational or transcendental.
What IS surprising is that fabulous approximations exist when the denominators are small compared to the degree of accuracy that is obtained.
Neither you nor Conway note the truly interesting part: these fabulous rational approximations are convergents to the continued fraction approximation to the square root of two.
If you could show some connection between the above proof and the well-known (periodic) continued fraction approximation to the square root of two, then it would make sense to include something about 17/12, above. Otherwise, I do not see the point — it has little to do with the proof, unless it had some historical interest.
17/12 is simply one of an infinite number of close (for the size of the denominator) rational approximations to the square root of two.
On the other hand, 22/7 is a famous historical example of a truly great rational approximation to pi. It’s value is:
3.1428…
while pi itself is (approximately):
3.14159265358…
Of course, 103993/33102 is far better than 22/7:
3.1415926530…
Interested readers might like to know more about continued fractions. The best intuitive, geometrical device that I know of for “seeing” them is the use of “Kline’s String”.
Look at the function y = x*SQRT(2) for positive x and y. This is simply a line in the plane. Note, however, that this line CANNOT intersect ANY integral lattice point, otherwise y/x would be a rational number equal to the square root of two and we know that such a number cannot exist.
But this line does come CLOSE to integral lattice points.
Imagine now, that the integral lattice points have tiny, tiny pegs in them and that the line, y = x*SQRT(2), is a thin, thin, string anchored at its end — infinitely far away. Now, holding it taut, move this string at the origin, upwards, along the y axis. The string will come to rest against those pegs — those integral lattice points — that are closet to it, and you will obtain a polygonal figure. Note that coordinates of these pegs — the lattice points that the string touches, will be excellent rational approximations to the square root of two, albeit their value will be higher than the actual square root of two. The farther up the polygonal figure you go the numbers get larger but the approximations to the square root of two become fantastically accurate.
You can move the string down the y axis and, similarly, the string will butt up against those lattice points that are excellent rational approximations to the square root of two, albeit they will be lower in value.
Indeed, these pegs — the integral lattice points that the string rests upon in both directions — will be EXACTLY the convergents computed from the continued fraction expansion to the square root of two.
Kline’s String is simply a beautiful GEOMETRIC way of seeing why the string will find these integral lattice points (the rational approximations).
It is rather mind boggling to think that the function y = x*SQRT(2) is an infinitely long line, yet it NEVER passes through an integral lattice point.
Prof. Richeson: Perhaps you will find the time to write a short intro to continued fractions and also include a nice graphical example of Kline’s string.
Meantime, interested readers can consult a truly wonderful book written decades ago by Davenport, titled “The Higher Arithmetic” (Number Theory):
When published, a review in the Bulletin of the American Mathematical Society stated that:
“Although this book is not written as a textbook but rather as a work for the general reader, it could certainly be used as a textbook for an undergraduate course in number theory and, in the reviewer’s opinion, is far superior for this purpose to any other book in English.”
The book explains continued fractions and Kline’s String far better than my awkward prose, above. In short, I hope I have done more good than harm by “publicizing” its existence.
Note, finally, that even though Kline’s string is in famous books, such as Davenport’s, many mathematicians — at least in my experience — are completely unaware of this truly wonderful geometric way of “seeing” the convergents to an irrational or transcendental number.
Peter Tennenbaum November 4, 2009
ERRATUM to the above post of Peter Tennenbaum’s. To wit:
I believe that “one should practice what one preaches” and, in this spirit, I readily admit to a stupid mistake in my attribution, above, concerning “Klein’s String”. I repeatedly misspelled it as “Kline’s String”.
Reader’s should note that this is a discovery of Felix Klein, the renowned mathematician (see, for example: http://en.wikipedia.org/wiki/Felix_Klein).
My version of H. Davenport’s “The Higher Arithmetic” was published in 1960 by Harper and Row in the United States of America. There, it says that “This book was first published in 1952 in the Mathematical and Physical Sciences division, edited by Sir George P. Thomson, of the Hutchinson & Company Limited, London.”
On page 114, reference 12, at the end of Chapter IV on Continued Fractions, Davenport writes:
“See Klein’s “Ausgewählte Kapitel der Zahlentheorie” (Teubner, 1907), pp. 17-25.”
When I wrote my post I was exhausted and under tremendous stress — enough to crush a large diamond into dust. I have been replicating, under a life and death situation (my wife’s rare ovarian cancer), the work of Novocure, an Israeli company, that is conducting Phase III trials at major institutions around the world of a revolutionary new cancer therapy — therapy now being given to patients suffering from glioblastoma, an aggressive brain cancer with an extremely poor prognosis. Note that Phase I breast cancer trials are pending.
Novocure’s work is based on EXTERNALLY placed capacitive conducting electrodes that, under the right conditions (applied frequency, geometric orientation, field strength, etc.), can make cancer cells explode into benign particles that are harmlessly reabsorbed into the body. Very roughly speaking, the technique works via a type of resonance effect although the actual bio-electrical-physics are far more complicated.
That said, I regard the above excuse as A POOR EXCUSE FOR MY EXTREMELY SHODDY SCHOLARSHIP. It is, however, an opportunity to show that I too make mistakes in attribution and, more importantly, that there is truly revolutionary work being done in cancer that’s been effective on EVERY cell type yet tested, in Petri dishes, rodents, and now human beings. Further, the therapy appears to be non-toxic, although it can be combined with various semi-toxic chemotherapeutic regimens to make it more efficacious.
A cursory Google search turned up little on “Klein’s String” but I obtained many more hits using the terms:
Klein continued fraction geometrical interpretation
Sadly, Wolfram’s Mathworld (http://mathworld.wolfram.com/ContinuedFraction.htmlhas) has a write-up that completely obfuscates the original idea (at least to me and my extremely limited mind). I doubt if Klein’s fabulous “string” will ever disappear from the modern literature but it would be an intellectual crime if less and less people were given an opportunity to experience the thrill of seeing it. To quote Davenport:
“A striking geometrical interpretation of the continued fraction for an irrational number was given by Klein in 1895”
In a sense, therefore, Klein’s String and Tennenbaum’s Proof are related.
I now sign off (for good, finally!) with a tremendous “Thank You” you to everyone who presented my father’s original work in a reasonable way, and to Steven J. Miller and David Montague for their truly beautiful extension of this line of development.
Peter Tennenbaum November 6, 2009
Terrific!
Given that “being irrational” is defined as “not being rational” (in other words “being rational implies false”), this is not a proof by contradiction. I’ve never encountered a proof of a negative statement that was not purely constructive.
Dear Peter,
I knew your dad, in 1980, when I was at IAS. He was a true mensch, one of the kindest, most caring people that I have met.
Penny Smith
Beautiful! It would speed up comprehension of the proof if it spelled out why the sides of the remaining pink and dark blue square must be integers. I had to think about that for a minute.